What Are Genetic Algorithm?
Genetic algorithm (GAs) are a class of optimization techniques inspired by the principles of natural selection and genetics. They form a subset of evolutionary algorithms, which are designed to solve complex problems by mimicking the process of biological evolution. GAs utilize a population-based approach to iteratively improve solutions to optimization problems, enabling efficient exploration of large search spaces.
The foundation of a genetic algorithm lies in its key components: populations, chromosomes, and fitness functions. A population consists of potential solutions, often represented as chromosomes. Each chromosome encodes a particular solution to the problem at hand. The GA algorithm begins by generating an initial population, which can be random or derived from previous knowledge of the problem. Over successive generations, these chromosomes undergo various genetic operations such as selection, crossover, and mutation.
Selection is the process by which the fittest individuals, or those with the highest fitness scores, are chosen to be parents for the next generation. This step mimics the natural selection process, where advantageous traits become more common in a population. Crossover combines the genetic information of two parent chromosomes to produce offspring, creating a diverse range of new solutions. Mutation introduces random changes to chromosomes to maintain genetic diversity, avoiding premature convergence on suboptimal solutions.
Fitness functions play a critical role in the execution of genetic algorithms. They assess how well each chromosome solves the problem, guiding the selection of more optimal solutions over iterations. Implementations of genetic algorithms often leverage programming languages such as Python, where libraries facilitate genetic optimization for various applications. By understanding the underlying concepts of the genetic algorithm, researchers and practitioners can apply these techniques to solve multi-objective optimization problems effectively, leading to innovative solutions inspired by nature.
Steps to Implement a Genetic Algorithm
Implementing a genetic algorithm involves a systematic approach that mimics natural evolution to solve optimization problems effectively. The first step is to clearly define the problem you aim to solve, as this will guide the entire process. This involves understanding the objectives you want to achieve and determining the parameters that will quantify success in the context of your problem.
Next, you need to encode potential solutions. This encoding process is crucial because the effectiveness of the genetic algorithm is largely determined by how solutions are represented. Common methods include binary encoding, which uses strings of 0s and 1s, and real-valued encoding, which directly represents solution characteristics as floating-point numbers. The choice of encoding should align with the nature of the problem and its constraints.
Once you have defined the problem and established your solution encoding, the next step is to initialize the population. A viable population ensures diversity, allowing the algorithm to explore various potential solutions. Typically, this involves generating a random set of individuals based on your chosen encoding scheme.
Subsequently, the algorithm applies selection, crossover, and mutation processes to evolve the population toward better solutions. Selection involves choosing the fittest individuals from the current population to serve as parents for the next generation. The crossover process combines the features of these parent solutions to create offspring, while mutation introduces random alterations to maintain genetic diversity and prevent premature convergence. These mechanisms should be applied iteratively, whereby each generation produces increasingly fit solutions.
Finally, you will continue with these iterations until an acceptable solution is achieved or a predefined stopping criterion is met. Metrics such as convergence to a fitness threshold or a maximum number of generations can dictate when the algorithm should terminate. By following these systematic steps, you can effectively implement a genetic algorithm, utilizing its power to optimize complex problems in various domains.
Key Components of Genetic Algorithms
To understand how genetic algorithms work, it’s essential to familiarize yourself with their key components:
1. Population
The population is a set of potential solutions to the problem. Each individual in the population represents a possible solution, often encoded as a chromosome.
2. Fitness Function
The fitness function evaluates how close a given solution is to the optimum. It assigns a fitness score to each individual in the population, which determines their likelihood of being selected for reproduction.
3. Selection
Selection is the process of choosing the best individuals from the population to create the next generation. Common selection methods include roulette wheel selection, tournament selection, and rank-based selection.
4. Crossover
Crossover is a genetic operator used to combine parts of two or more solutions to create new ones. It mimics the biological process of reproduction and helps in exploring new regions of the search space.
5. Mutation
Mutation introduces random changes to the individuals in the population. It helps maintain genetic diversity and prevents the algorithm from converging too quickly to a suboptimal solution.
Genetic Algorithm Workflow
The workflow of a genetic algorithm can be summarized in the following steps:
- Initialization: Create an initial population of potential solutions.
- Evaluation: Evaluate the fitness of each individual in the population.
- Selection: Select the best individuals based on their fitness scores.
- Crossover: Perform crossover to create new offspring.
- Mutation: Apply mutation to the offspring.
- Replacement: Replace the old population with the new population.
- Termination: Repeat the process until a termination condition is met (e.g., a maximum number of generations or a satisfactory fitness level).
Genetic Algorithm in python
Implementing a genetic algorithm in Python is relatively straightforward, thanks to libraries like DEAP and PyGAD. Below is a simple example to illustrate the basic concepts:
import random
def fitness(individual):
return sum(individual),
def create_individual():
return [random.randint(0, 1) for _ in range(10)]
def mutate(individual):
index = random.randint(0, len(individual) - 1)
individual[index] = 1 - individual[index]
population = [create_individual() for _ in range(10)]
for generation in range(100):
population = sorted(population, key=lambda ind: fitness(ind), reverse=True)
next_generation = population[:2]
for _ in range(8):
parent1, parent2 = random.sample(population[:5], 2)
child = parent1[:5] + parent2[5:]
mutate(child)
next_generation.append(child)
population = next_generationPython Assignment Help
If you’re looking for Python assignment help, you’re in the right place! I offer expert assistance with Python homework help, covering everything from basic coding to complex simulations. Whether you need help with a Python assignment, debugging code, or tackling advanced Python assignments, I’ve got you covered.
Why Trust Me?
- Proven Track Record: Thousands of satisfied students have trusted me with their Python projects.
- Experienced Tutor: Taught Python programming to over 1,000 university students worldwide, spanning bachelor’s, master’s, and PhD levels through personalized sessions and academic support
- 100% Confidentiality: Your information is safe with us.
- Money-Back Guarantee: If you’re not satisfied, we offer a full refund.
Genetic Algorithm in MATLAB
The following is the problem that we are going to solve using MATLAB
% Define the Inequality Constraints
A = [-1, -2, 1
-4, -1, -3
2, 1, 1];
b = [14; -33; 20];
% Define the Equality Constraints
Aeq = [1, 0, 1];
beq = 6.5;
% Define Bounds
lb = [0; 0; 0]; % lower bounds for x1, x2, x3
ub = [Inf; Inf; 1]; % x1 continuous, x2 unbounded, x3 binary (0 or 1)
% Set Integer Constraints for GA (only x2 should be integer)
intCon = [ 2 3]; % This tells GA that x2 should be integer
% Set Options for Genetic Algorithm
options = optimoptions('ga', ...
'PopulationSize', 20, ...
'MaxGenerations', 10, ...
'Display', 'iter', ...
'PlotFcn', @gaplotbestf); % Plots the best function value at each generation
% Run the Genetic Algorithm
[x, fval] = ga(@objectiveFunction, 3, A, b, Aeq, beq, lb, ub, [], intCon, options);
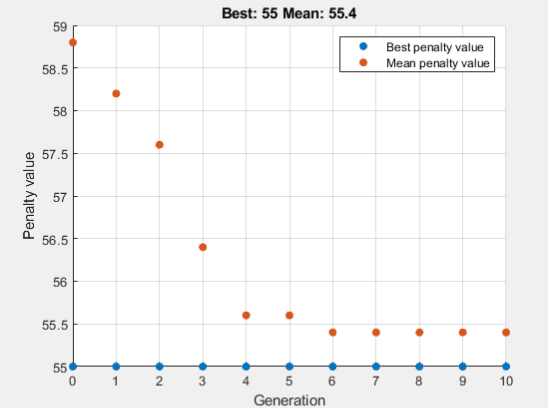
- PopulationSize’: This defines the number of individuals (solutions) in each generation. By setting ‘PopulationSize’, 20, we’re telling GA to use 20 individuals per generation. In a GA, a population is a set of possible solutions. A larger population size can increase the diversity of solutions but also requires more computation.
- ‘MaxGenerations’: This specifies the maximum number of generations GA will run. A generation is essentially a cycle where the algorithm selects, crosses over, and mutates individuals to produce a new set of solutions. Here, MaxGenerations is set to 10, so GA will stop after 10 generations if it hasn’t found the optimal solution yet.
- ‘Display’: The ‘Display’, ‘iter’ option means that GA will print information about each generation as it progresses. ‘iter’ stands for “iteration,” and it allows you to see how the best solution evolves after each generation.
- ‘PlotFcn’: This is the function that MATLAB uses to plot the best fitness (objective function) value at each generation. Setting it to @gaplotbestf provides a plot showing the best solution found in each generation, allowing you to visualize the algorithm’s progress over time.
Learn MATLAB with Free Online Tutorials
Explore our MATLAB Online Tutorial, your ultimate guide to mastering MATLAB! his guide caters to both beginners and advanced users, covering everything from fundamental MATLAB concepts to more advanced topics.
The History and Evolution of Genetic Algorithm
Genetic algorithms, a subset of evolutionary algorithms, were conceived in the 1970s by the visionary computer scientist John Holland. Holland’s pioneering work laid the groundwork for a new computational methodology grounded in the principles of natural selection and genetics. By mimicking Darwinian evolutionary processes, Holland aimed to create algorithms that could efficiently search through complex solution spaces to optimize and solve problems.
The conceptual framework established by Holland emphasized the importance of mechanisms such as selection, crossover, and mutation, which are intrinsic to biological evolution. In the decades following Holland’s initial propositions, the genetic algorithm (GA) gained traction, fueled by the increasing availability of computational resources. This era marked significant milestones, as advancements in hardware allowed researchers to test and refine genetic optimization algorithms more extensively. As computational power surged, so too did the sophistication and applications of the GA algorithm across diverse fields, including engineering, economics, and artificial intelligence.
MATLAB Assignment Help
If you’re looking for MATLAB assignment help, you’re in the right place! I offer expert assistance with MATLAB homework help, covering everything from basic coding to complex simulations. Whether you need help with a MATLAB assignment, debugging code, or tackling advanced MATLAB assignments, I’ve got you covered.
Why Trust Me?
- Proven Track Record: Thousands of satisfied students have trusted me with their MATLAB projects.
- Experienced Tutor: Taught MATLAB programming to over 1,000 university students worldwide, spanning bachelor’s, master’s, and PhD levels through personalized sessions and academic support
- 100% Confidentiality: Your information is safe with us.
- Money-Back Guarantee: If you’re not satisfied, we offer a full refund.
By the late 1980s and early 1990s, the algorithm of genetic algorithm had expanded beyond theoretical research. The increasing interest in machine learning and artificial intelligence further propelled the application of genetic algorithms. Researchers began integrating GAs into complex systems for tasks such as optimization and scheduling. This ability to adapt and find optimal solutions in real-time led to the popularization of the genetic algorithm in both academic and industrial contexts.
In recent years, the growth of programming languages like Python has made genetic algorithms more accessible to a broader audience. With libraries developed specifically for genetic optimization in Python, such as DEAP and PyGAD, practitioners can implement and test examples for genetic algorithms with relative ease. This ongoing evolution of genetic algorithms continues to inspire innovative solutions, illustrating the profound impact of natural principles on technological advancement.
Key Concepts Behind Genetic Algorithm
Genetic algorithms (GAs) are heuristic search algorithms inspired by the principles of natural selection and genetics. They formulate solutions to optimization and search problems through a process resembling biological evolution. To understand genetic algorithms, it’s essential to grasp several key concepts such as selection, crossover, mutation, and fitness evaluation, each playing a critical role in the algorithm’s performance.
The first component, selection, involves choosing the most suitable candidates from a current population of potential solutions. This process can employ various methods, like roulette wheel selection or tournament selection, which focus on the concept of survival of the fittest. The objective is to ensure that better-performing solutions have a higher probability of contributing to the next generation, aligning with the algorithm of genetic algorithm principles.
Next, crossover, or recombination, is the mechanism whereby parent solutions exchange genetic material to produce offspring. This process is akin to biological reproduction, fostering diversity within the population. Effective crossover strategies, such as one-point or multi-point crossover, can significantly influence the genetic algorithm’s optimization capabilities, resulting in new solutions that may outperform their predecessors.
Mutation introduces random changes to an individual’s genetic makeup in the search space. This chaotic element is essential as it prevents the algorithm from converging prematurely on suboptimal solutions. In the context of genetic optimization with Python, mutation rates must be carefully balanced to facilitate exploration while maintaining sufficient levels of exploitation of the best solutions.
Lastly, the fitness evaluation function assesses how well each solution meets the specified problem objectives. This evaluation is crucial for guiding selection processes, effectively steering the evolutionary pathway. A strong fitness function ensures that the genetic algorithm and machine learning techniques work synergistically, leading to the discovery of optimal or near-optimal solutions.
Applications of Genetic Algorithm
Genetic algorithms (GAs) are broadly applicable across a variety of industries, significantly enhancing problem-solving capabilities where traditional methods may fall short. Their foundation in nature’s evolutionary processes makes them particularly effective for optimization tasks. One of the most prominent fields utilizing genetic algorithm optimization is artificial intelligence, where they contribute to adaptive systems that learn and improve over time. These algorithms allow systems to evolve solutions to complex problems, making them pivotal in areas such as robotics and intelligent data processing.
In the realm of machine learning, the GA algorithm is instrumental in feature selection—a critical process for improving model performance. By identifying the most relevant features, genetic algorithms facilitate the development of more accurate predictive models. Additionally, in scenarios involving large datasets, genetic algorithm optimization can simplify data management and enhance the efficiency of learning algorithms.
Another noteworthy application of genetic algorithms is within bioinformatics, where they are employed for sequence alignment and genome mapping. The algorithm of genetic algorithm enables researchers to optimize search processes for genetic data, significantly contributing to advancements in personalized medicine and disease modeling. Moreover, their application extends to engineering design, facilitating the creation of innovative solutions by rapidly generating and evaluating design alternatives, thereby streamlining development cycles.
Genetic algorithms have also emerged as a powerful tool for solving multi-objective optimization problems. For example, engineers can leverage genetic algorithm multi-objective optimization to balance conflicting objectives, such as maximizing performance while minimizing costs and material use. This versatility illustrates how GA algorithms serve not just in theoretical contexts, but also as practical utilities that drive efficiency and innovation across multiple disciplines.
Advantages and Disadvantages of Genetic Algorithm
Genetic algorithms (GA) are a class of optimization techniques inspired by the principles of natural selection and genetics. Their strength lies in various advantages that make them suitable for solving complex problems. One significant benefit of the genetic algorithm is its adaptability. GAs can efficiently evolve solutions to problems that involve a vast search space, adjusting to changes in criteria or environments over time. This dynamic response to evolving challenges is particularly advantageous in real-world applications where conditions are not static.
Another key advantage of the GA algorithm is its parallelism. By maintaining a population of potential solutions, genetic algorithms can explore multiple areas of the solution space simultaneously. This ability to perform simultaneous evaluations can often lead to quicker convergence towards optimal solutions compared to traditional methods that explore paths sequentially.
An essential feature of genetic algorithms is their decreased susceptibility to local optima. Unlike gradient-based optimization methods that can become stuck in local minima, genetic algorithms employ a heuristic approach which makes them more likely to find a global optimum, especially in multi-objective optimization scenarios. The flexibility to customize the algorithm enables researchers and practitioners to tailor approaches based on the specific problem domain.
Despite these advantages, genetic algorithms come with certain limitations. One primary drawback is the computational cost associated with evaluating many potential solutions. As the problem size increases, the need for substantial computational resources can become a barrier, especially for real-time applications. Additionally, the complexity of tuning the parameters of a genetic algorithm can pose challenges; improper settings can lead to suboptimal performance. Thus, while genetic algorithms provide robust frameworks for optimization, they require careful consideration and fine-tuning to ensure effective outcomes in genetic optimization Python applications or in conjunction with machine learning technologies.
Real-World Examples of Genetic Algorithms in Action
Genetic algorithms (GA) have become a pivotal tool across various industries due to their efficiency in solving complex optimization problems. One prominent application lies in transportation logistics, where companies leverage these algorithms to optimize delivery routes. By simulating the evolutionary process of natural selection, the algorithm identifies the most efficient paths, thereby reducing fuel consumption and improving overall delivery times. For instance, a logistics company, using a genetic algorithm implemented in Python, was able to minimize operational costs significantly by optimizing its fleet routes based on demand fluctuations and traffic patterns.
Another compelling example is found in the realm of artificial intelligence, specifically in developing and evolving neural network topologies. The algorithm of a genetic algorithm can be employed to search and select optimal architectures for neural networks. By employing genetic optimization techniques, researchers can evolve networks to perform specific tasks more effectively, such as image recognition or natural language processing. This process not only enhances the performance of the networks but also reduces training time, showcasing the practical and innovative applications of genetic algorithms within machine learning.
Scheduling is yet another area where genetic algorithms demonstrate significant usefulness. Complex scheduling tasks, such as workforce allocation or production scheduling, pose challenges that are well-suited for the adaptive nature of genetic algorithms. By modeling the problem as a population of schedules and applying selection, crossover, and mutation processes, optimal solutions emerge over successive generations. An example for a genetic algorithm in this domain includes a manufacturing firm that improved its production schedule, resulting in increased efficiency and reduced downtime.
Thus, genetic algorithms not only simplify complex problem-solving processes but also contribute to vital advancements in diverse fields, firmly establishing their role in contemporary technological innovation.
Need Help in Programming?
I provide freelance expertise in data analysis, machine learning, deep learning, LLMs, regression models, NLP, and numerical methods using Python, R Studio, MATLAB, SQL, Tableau, or Power BI. Feel free to contact me for collaboration or assistance!
Follow on Social
Future Trends in Genetic Algorithms
As technology continues to advance, the utilization of genetic algorithms (GAs) is expected to expand, leading to innovative applications across a variety of fields. One significant trend is the development of hybrid algorithms that combine genetic algorithms with other optimization techniques. These hybrid forms take advantage of the strengths of both algorithms, enhancing performance in complex problem-solving scenarios. For instance, incorporating elements from machine learning into the genetic algorithm can lead to improved efficiency and more effective solutions in tasks such as pattern recognition and predictive modeling.
Moreover, advancements in computational techniques are set to further streamline the implementation of genetic algorithms. With the growing power of computing resources and the advent of quantum computing, the algorithm of genetic algorithm is anticipated to undergo significant improvements. These enhancements will not only increase the speed of the GA algorithm but also allow for complex problem-solving that was previously unattainable. As a result, larger datasets can be processed more efficiently, enabling the genetic optimization python libraries to tackle increasingly sophisticated scenarios.
Future applications of genetic algorithms in fields such as artificial intelligence and complex system optimization will be pivotal. The versatility of the genetic algorithm python framework presents an attractive option for developers and researchers looking for robust methods to solve multi-objective optimization problems. As more industries recognize the potential of the algorithm genetic python in the context of big data, the demand for adaptable GAs will rise. Anticipated progress in areas such as automated machine learning and dynamic resource management is set to expand the horizons for genetic algorithm optimization and solidify its relevance in upcoming technological landscapes.
In conclusion, the future of genetic algorithms is promising, with numerous trends and developments anticipated to enhance their functionality and application. As these innovations unfold, they will undoubtedly shape the way complex problems are approached in the realms of artificial intelligence and beyond.
Getting Started with Genetic Algorithms: Resources and Tools
Venturing into the world of genetic algorithms (GAs) can be an exhilarating journey, as these algorithms mimic natural evolutionary processes to solve complex optimization problems. For those eager to learn more, a variety of resources and tools are available to facilitate understanding and application of the algorithm of genetic algorithm.
One of the best starting points is online courses that offer structured learning environments. Platforms like Coursera, edX, and Udacity provide courses focusing on genetic algorithms in the context of artificial intelligence and machine learning. These courses often incorporate practical examples for genetic algorithm applications, making them valuable for both beginners and those looking to deepen their knowledge.
For hands-on practice, numerous libraries are designed specifically for implementing genetic algorithms in Python. The popular library DEAP (Distributed Evolutionary Algorithms in Python) offers a comprehensive framework for genetic algorithm implementation. Similarly, PyGAD is another robust library that simplifies the development of GA algorithms, making it easier to integrate them with various optimization tasks. The comprehensive documentation and user guides provided by these libraries are exceedingly beneficial for beginners.
In addition to formal resources, engaging with the online community can significantly enhance one’s understanding. Forums such as Stack Overflow and Reddit’s r/MachineLearning offer platforms where enthusiasts and experts exchange ideas, algorithms, and troubleshooting tips. Participating in discussions can provide insights into practical genetic optimization python applications, and even expose users to advanced strategies like genetic algorithm multi-objective optimization.
Furthermore, numerous research papers and eBooks delve into the theoretical aspects of genetic algorithms and machine learning, providing a richer context for their application. This amalgamation of resources supports learners in navigating through both foundational theory and practical implementation of the algorithm genetic python.