Newton Raphson Method in MATLAB

Introduction to the Newton Raphson Method

The Newton-Raphson method is a powerful numerical technique used for finding successively better approximations to the roots (or zeros) of a real-valued function. It is particularly significant in numerical analysis due to its efficiency and speed in converging to a solution, making it a preferred choice among engineers, mathematicians, and scientists. The essence of the method lies in its iterative approach, which utilizes the tangent line at a given point to approximate the function’s root and MATLAB can implement Newton Raphson Method. Starting with an initial guess, the algorithm refines this guess by evaluating the function and its derivative, thus enhancing the accuracy of the approximation with each iteration.

This method can be applied to a wide range of problems, from solving non-linear equations to optimizing functions. The Newton-Raphson method’s effectiveness is often demonstrated through its rapid convergence properties, especially when compared to other root-finding algorithms like the bisection method or fixed-point iteration. Its utility can be seen in various fields, including physics, engineering, and finance, where the accurate identification of roots is crucial for theoretical and practical applications.

Understanding the Mathematical Foundation

The Newton-Raphson method, an essential technique in numerical analysis, primarily aims to find successively better approximations of the roots of a real-valued function. The method is grounded in two fundamental concepts: derivatives and fixed-point iteration. At its core, the approach utilizes the derivative of a function to facilitate rapid convergence toward a solution. The principle lies in the formulation of tangent lines; when one computes the tangent to the function at a given point, the intersection of this tangent with the x-axis provides a new approximation for the root.

The mathematical expression that underpins the Newton-Raphson process is expressed as:

x_n+1 = x_n – f(x_n) / f'(x_n)

Here, x_n represents the current approximation, while x_n+1 is the next iterative approximation. The function f denotes the target function, and f’ symbolizes its derivative. Each iteration effectively refines the result by utilizing the local linearization of the function around the current approximation. This strategy fosters a quick convergence, particularly when the initial guess is sufficiently close to the actual root.

Another pivotal aspect is the concept of fixed-point iteration. In this method, one seeks a fixed point x such that g(x) = x, where g can be derived from rearranging the original function. This approach allows the integration of iterative methods alongside the applicability of the Newton-Raphson method. As such, understanding these mathematical foundations arms practitioners with the knowledge necessary to implement the method effectively in MATLAB.

Mastering these fundamental concepts is crucial before delving into the practical applications of the Newton-Raphson method. The integration of derivatives offers a framework where computational efficiency is maximized, setting the stage for practical coding exercises and further exploration within MATLAB.

How the Newton-Raphson Method Works

At its core, the method uses the tangent of a function to approximate its root. Starting with an initial guess x_0​, the formula

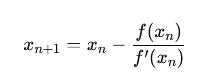
iteratively refines the guess until it converges to the root. Here’s what happens step by step:

1. Choose an initial guess: Start close to where you think the root might be.
2. Evaluate the function and its derivative: Use f(x)and f′(x)
3. Update the guess: Apply the formula above.
4. Repeat until convergence: Stop when the difference between guesses is small enough.

Practical Use Cases for the Newton Raphson Method in MATLAB

1. Engineering Applications: Solve stress-strain relationships in materials.
2. Machine Learning: Optimize hyperparameters in a cost function.
3. Business Analytics: Model consumer behavior using nonlinear equations.

These scenarios showcase the versatility of this technique, whether you’re working with physical systems or abstract data models.

Setting Up MATLAB for Implementation

To effectively implement the Newton-Raphson method in MATLAB, the first step is to ensure that the software is properly installed. MATLAB is a powerful programming environment used for numerical computation and visualization. It can be downloaded from MathWorks’ official website, where users can choose to download a trial version or purchase a license. The version of MATLAB you choose should be compatible with your operating system and requirements. Once the installation is complete, you will have access to the MATLAB desktop interface, which contains essential tools and capabilities for your computational tasks.

After installing MATLAB, it is crucial to configure the environment for optimal performance. Start by familiarizing yourself with the MATLAB workspace, command window, and editor. Ensuring that your paths are set correctly can significantly enhance your experience, allowing for the seamless integration of scripts and functions. To configure paths, use the ‘Set Path’ option in the Home tab, where you can add custom directories or remove those that are not necessary.

Additionally, for utilizing the Newton-Raphson method effectively, specific toolboxes may be required. The Optimization Toolbox is particularly useful, as it includes numerous algorithms that can complement the Newton-Raphson method. Check if you have access to this toolbox by navigating to the “Add-Ons” section in MATLAB, where you can install or acquire additional toolboxes as needed.

Finally, once the setup is complete, consider practicing with sample scripts that implement the Newton-Raphson method. There are many resources available online, including user manuals and community forums. Engaging with these resources can deepen your understanding and provide insights into potential challenges you may encounter when developing your own implementations in MATLAB.

For additional assistance, we invite you to explore our comprehensive blog article featuring 60 detailed MATLAB examples. These examples are designed to help you enhance your understanding of MATLAB’s functionalities and application in various fields. Each example is thoughtfully selected to cover a range of topics, from basic syntax and operations to more advanced programming techniques, ensuring that learners at all levels can benefit from them. Whether you’re just beginning or looking to refine your skills, this resource will provide valuable insights and practical knowledge.

Step-by-Step Implementation of the Newton Raphson Method

The Newton-Raphson method is a powerful technique for finding roots of equations, and its implementation in MATLAB can be straightforward if proper attention is paid to the code structure. To begin, the essential variables must be defined, including the function for which the root is sought, its derivative, and an initial guess. In MATLAB, the function can be defined with an anonymous function as follows:

f = @(x) x^2 - 2; % Example function

Next, its derivative is similarly defined:

df = @(x) 2*x; % Derivative of the function

With the function and its derivative properly set up, the next step involves initializing the guess and specifying a tolerance for convergence. This is crucial for ensuring that the method stops iterating when an adequate level of precision has been achieved:

x0 = 1; % Initial guess

tol = 1e-6; % Tolerance

Now, we can implement the iterative process of the Newton-Raphson method. A while loop in MATLAB will execute until the absolute difference between consecutive approximations is below the specified tolerance:

while true
x1 = x0 - f(x0)/df(x0); % Newton-Raphson formula
if abs(x1 - x0) < tol
break;
end
x0 = x1;
end

During this implementation, it is critical to handle potential pitfalls. For instance, if the derivative is zero, the method will encounter an undefined operation. Use can find the derivative of a function in using MATLAB diff function. To mitigate this, adding a conditional check can prevent division by zero errors:

if df(x0) == 0
error('Derivative is zero. No solution found.');
end

In conclusion, the MATLAB Newton-Raphson implementation involves defining the function and its derivative, setting initial parameters, and executing the iterative method with careful consideration of potential obstacles, thus enabling users to adeptly navigate any challenges they might encounter.

1. Setup and Prerequisites

• Install MATLAB.
• Familiarize yourself with basic MATLAB syntax for defining functions.
• Prepare the equation f(x) and its derivative f′(x).

2. Write the Core Algorithm

Define f(x) and f′(x) as anonymous functions:

f = @(x) x^2 - 2;       % Example: Finding the square root of 2
df = @(x) 2*x;          % Derivative of f(x)

3. Iterative Process

Initialize variables and iterate using while loop or for loop in MATLAB :

x0 = 1;                 % Initial guess
tol = 1e-6;             % Tolerance for convergence
max_iter = 100;         % Maximum number of iterations
iter = 0;

while iter < max_iter
    x1 = x0 - f(x0)/df(x0);  % Newton-Raphson formula
    if abs(x1 - x0) < tol    % Check for convergence
        break;
    end
    x0 = x1;
    iter = iter + 1;
end

disp(['Root found: ', num2str(x1)]);

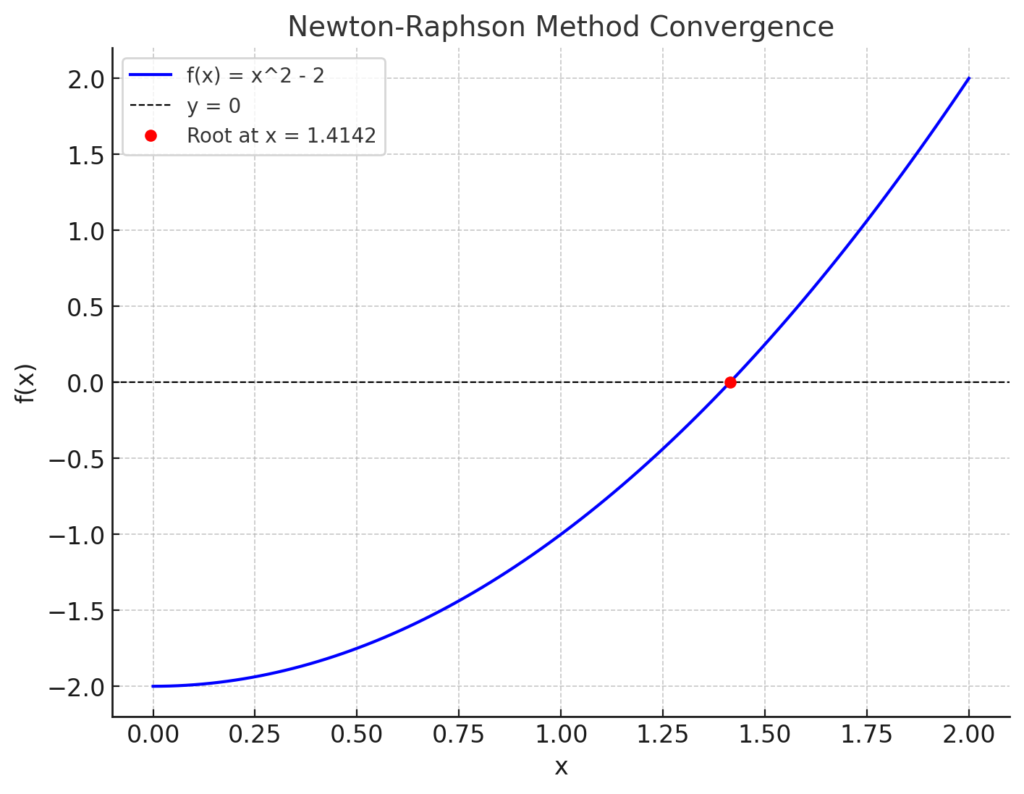
Visualization

Visualize convergence to the root using MATLAB plotting functions:

x = linspace(0, 2, 100);
plot(x, f(x));
hold on;
plot(x1, f(x1), 'ro');  % Mark the root
title('Newton-Raphson Method Convergence');
xlabel('x');
ylabel('f(x)');
grid on;

Real-World Applications of the Newton Raphson Method using MATLAB

The Newton Raphson method is a versatile numerical technique widely used in various fields, offering efficient solutions to complex problem-solving scenarios. Its primary strength lies in its ability to quickly converge to roots of equations, making it valuable in engineering, finance, and data analysis. In engineering, for example, it is frequently employed in optimizing designs and systems, particularly in structural analysis and control systems. Engineers rely on the method to find critical points such as load capacities or equilibrium states of structures, ensuring safety and functionality.

In the field of finance, the Newton Raphson method is instrumental in solving equations that arise in financial modeling, such as finding interest rates or analyzing investment performance. The method simplifies the calculations involved in complex financial instruments, allowing analysts to derive necessary parameters rapidly. This capability is particularly beneficial when evaluating options pricing models or optimizing investment returns, where accurate computations can yield significant advantages.

Furthermore, in data analysis, the Newton Raphson method aids in various optimization tasks, such as fitting statistical models to real-world data. It is advantageous in scenarios where maximizing or minimizing certain objectives is crucial, for instance, in machine learning for training algorithms or in statistical inference to determine the best-fit parameters. The ability to swiftly locate the optimal solutions simplifies the analytical processes and enhances the efficiency of data-driven decision-making.

The distinctive qualities of the MATLAB implementation of the Newton Raphson method also contribute to its attractiveness. By utilizing MATLAB’s powerful computational capabilities, users can efficiently leverage the method for large data sets and complex equations. As such, proficiency in the Newton Raphson method within MATLAB not only aids individual practitioners but also serves to enhance the operational efficiency of businesses across various sectors, making it an indispensable tool for modern problem-solving.

Learn MATLAB with Online Tutorials

Explore our MATLAB Online Tutorial, your ultimate guide to mastering MATLAB! Whether you’re a beginner or an advanced user, this guide covers everything from basic MATLAB concepts to advanced topics

Optimizing the Newton Raphson Method for Performance

The Newton-Raphson method is a powerful numerical technique for finding roots of real-valued functions, but its performance can be significantly enhanced through various optimization techniques when implemented in MATLAB. One primary focus in optimizing the MATLAB Newton-Raphson algorithm is to improve convergence speed. This can be achieved by refining the initial guess for the root. A closer starting point often leads to fewer iterations and quicker convergence. To identify a suitable initial guess, graphical techniques like plotting the function can be utilized, or analytical insights about the behavior of the function can be examined.

Handling edge cases is another critical aspect of optimization. The traditional Newton Raphson method may fail or exhibit poor performance for functions with inflection points or derivative values that are zero, leading to undefined behaviors. To mitigate these issues, one can incorporate fallback strategies. For instance, if the derivative at a guess is close to zero, a line search method or a hybrid approach that combines bisection with Newton’s method can be employed. Such strategies provide a more reliable path towards convergence, ensuring that the algorithm does not become stuck or diverge.

Furthermore, refining the algorithm itself can lead to performance gains. This might involve using variable step sizes, where the next guess is adjusted based on past iterations, or implementing a multi-dimensional approach when dealing with higher-order systems. Additionally, MATLAB’s built-in functions for optimization, such as the use of vectorized operations, can significantly reduce computation time. By harnessing MATLAB’s computational strengths, especially when dealing with large datasets or complex functions, one can execute the Newton Raphson method more efficiently.

By focusing on these optimization techniques, one can fully leverage the capabilities of the Newton Raphson method in MATLAB, leading to enhanced coding skills and improved application performance.

Common Challenges and How to Overcome Them

The Newton-Raphson method, despite its efficiency, can present several challenges to student when utilized within MATLAB. One prominent issue that practitioners encounter is the problem of convergence. For the method to converge to a solution, the initial guess is crucial. If the starting point is too far from the actual root or if the function is not well-behaved near that point, convergence may fail, leading to erroneous results or divergence. To mitigate this risk, it is recommended to conduct a preliminary analysis of the function to identify intervals where roots are likely to exist. Using graphical methods, such as plotting the function, can provide a visual reference to determine a suitable starting point.

Another frequent challenge relates to the selection of the derivative in the Newton Raphson method. Inaccurately calculating the derivative can lead to missteps in iteration, thereby influencing the convergence negatively. Therefore, ensuring that the derivative is correctly computed and verified is essential. Additionally, while MATLAB allows for symbolic differentiation, it’s prudent to consider numerical approximations when dealing with complex functions, as this can enhance reliability in calculations.

Potential exceptions, such as reaching a stationary point where the derivative is zero, also pose challenges during the iterative process. When this occurs, the Newton Raphson method may not proceed effectively, resulting in an undefined or infinite value. To handle such exceptions, users can adopt modified approaches, such as switching to alternative numerical methods, including the Secant Method or Bisection Method, which are robust in such scenarios.

In summary, being cognizant of these challenges and implementing strategic measures can significantly enhance the efficacy of using the Newton-Raphson method in MATLAB. By meticulously selecting starting points, ensuring accurate derivatives, and preparing for exceptional cases, users can successfully tackle common obstacles and improve their experience with this powerful mathematical tool.

Extending the Newton Raphson Method to Complex Functions

The Newton Raphson method is not limited to real-valued functions; it can also be effectively extended to complex functions. This versatility is particularly advantageous for advanced users who are interested in finding roots of equations involving complex variables. The foundational principles of the method remain the same, wherein the iterative formula is derived from the function’s derivative. However, the implementation necessitates some adjustments to accommodate the intricacies of complex analysis.

When adapting the Newton Raphson method for complex functions, the iterative formula can be expressed as:

x_n+1 = x_n – f(x_n) / f'(x_n)

In this equation, both f(x) and its derivative f'(x) can comprise complex variables. Thus, it is vital to ensure that both the function and its derivative are appropriately defined for complex numbers. Typically, MATLAB provides robust support for complex arithmetic, enabling users to seamlessly apply the Newton-Raphson method without extensive modifications.

One primary challenge in using the Newton Raphson method with complex functions is ensuring the convergence of the iterative process. Since the complex plane is multi-dimensional, the choice of initial guess significantly influences the outcome. Users may need to experiment with various starting points to find the root effectively. Furthermore, the method can struggle with functions that exhibit multiple roots or that are highly oscillatory near the root.

To enhance the reliability and efficacy of the method, it can be beneficial to visualize the convergence of each iteration in MATLAB. By employing graphical representations, users can gain insights into the behavioral patterns of complex functions, ultimately improving their understanding and application of the Newton Raphson method. This adaptation paves the way for exploring a broader range of mathematical problems solving in complex analysis.

Conclusion and Resources for Further Learning

The Newton Raphson method serves as a fundamental technique in both data science and programming for solving equations efficiently. Throughout this guide, we have explored the underlying principles of this method, as well as its implementation in MATLAB or Python. By leveraging this iterative technique, users can achieve rapid convergence to the roots of real-valued functions, making it an invaluable tool for engineers, mathematicians, and data scientists alike.

One primary takeaway from our exploration is the versatility and efficacy of the MATLAB Newton Raphson method. By understanding how to implement this algorithm, practitioners can solve complex equations that may otherwise pose a significant challenge. Moreover, we have highlighted the importance of initial guesses and convergence criteria in ensuring the method’s success. Such factors are critical in avoiding pitfalls like divergence, which can occur if the initial estimates are not thoughtfully chosen.

To further enhance your understanding of the Newton-Raphson method and its applications in MATLAB, several resources are recommended. Online platforms such as Coursera and edX offer specialized courses that cover both the theoretical aspects and practical implementations of numerical methods, including the Newton-Raphson technique. Additionally, classic textbooks like “Numerical Methods for Engineers” by Chapra and Canale provide in-depth discussions of algorithms alongside MATLAB examples.

Lastly, MATLAB’s official documentation serves as a critical reference point. Further you can take help from our blog article which contains 60 matlab examples to learn from. It not only includes practical guides on how to implement the Newton-Raphson method but also presents a wealth of examples that can facilitate deeper learning. Engaging with these resources will aid in mastering the Newton-Raphson method and expanding one’s skill set in numerical analysis and computational programming.

Learn to Implement Euler Method in MATLAB

One of the key advantages of the Euler method is its simplicity and ease of implementation, particularly in programming environments such as MATLAB. Learn to Implement Euler Method in MATLAB

The method allows for a rapid computation of approximate values, making it a popular choice for introductory courses in numerical methods. the Euler method, named after the Swiss mathematician Leonhard Euler, is a fundamental numerical technique widely used in mathematical analysis for solving ordinary differential equations (ODEs).