MATLAB Diff function – A Beginners Guide

Introduction to MATLAB Diff

MATLAB diff function is an essential tool utilized in the realms of data analysis and programming. Primarily, it calculates the differences between adjacent elements in an array, offering valuable insights into trends and behaviors of data sets. The significance of understanding this function goes beyond mere computation; it equips users with the ability to conduct thorough analyses of datasets, enabling them to unlock patterns and anomalies that are crucial for informed decision-making.

Target audiences for this function include a diverse range of professionals, students, and small business owners who seek to harness the power of data. For data scientists, the diff function becomes a foundational skill in time-series analysis, as it helps in identifying changes over time, thus facilitating predictive modeling. Students who are pursuing technical disciplines find a practical application for the diff function, as it serves as a stepping stone towards mastering larger concepts in calculus and data operations. Meanwhile, small business owners can leverage the diff function to analyze sales or operational data, identifying growth trends or areas needing improvement with minimal effort.

This blog aims to address the pressing needs of these groups by focusing on practical applications and real-world relevance of the MATLAB diff function. By mastering this tool, users can efficiently resolve specific technical challenges, improve their analytical skills, and find meaningful interpretations of their data. Through a blend of theoretical understanding and hands-on practical examples, this guide aspires to empower readers to utilize MATLAB’s diff effectively, transforming raw data into actionable insights. The journey of mastering data analysis commences with a comprehensive grasp of MATLAB diff; this article will serve as a detailed roadmap to that endeavor.

Understanding the Basics of Differentiation

Differentiation is a fundamental concept in mathematics, particularly in calculus, that refers to the process of finding the derivative of a function. A derivative represents the rate at which a quantity changes; essentially, it provides a measure of how a function’s output changes in response to changes in its input. This concept is crucial in many fields, especially data science and engineering, where understanding dynamic systems and behaviors is essential.

At its core, the derivative is defined as the limit of the average rate of change of a function as the interval approaches zero. This is mathematically expressed as:

f'(x) = lim (h → 0) [f(x+h) – f(x)] / h

In simpler terms, the derivative at a specific point on a graph provides the slope of the tangent line to the curve at that point, indicating how steeply the function rises or falls. For example, in data science, if we examine a stock price over time, the derivative can give us insights into the stock’s volatility, helping investors make informed decisions.

The importance of differentiation extends to various applications, such as optimization problems where one aims to maximize or minimize functions, and in predictive modeling, where understanding the rate of change can lead to better forecasting. For instance, in engineering, knowing how forces change over time can significantly impact design and safety considerations.

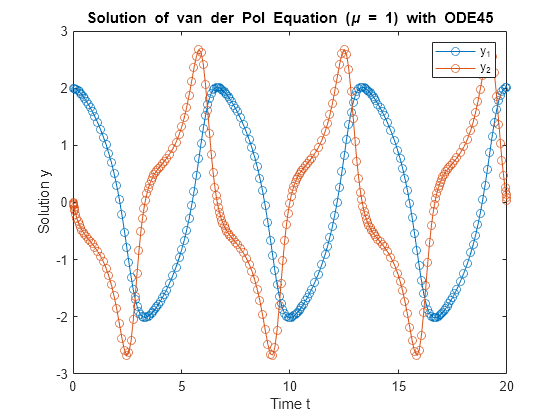
Getting Started with MATLAB Diff Function

The diff function in MATLAB is a powerful tool used for numerical differentiation and calculating differences between elements in an array. To begin using it effectively, it is essential to understand its syntax and how it can apply to various types of input data.

The basic syntax in MATLAB of the diff function is straightforward:

Y = diff(X)

Here, X represents the input array, which can be a vector or matrix, and Y will hold the result of the differences computed from X. For vectors, the function computes the differences between adjacent elements, while for matrices, it computes the differences along each column.

For example, consider a simple vector:

X = [2, 4, 6, 8]
Y = diff(X);
This results in Y = [2, 2, 2]

This shows that the difference between each pair of adjacent elements in X is consistently 2.

Additionally, the diff function can handle multi-dimensional arrays. In such cases, specifying the dimension would be useful. For instance:

Y = diff(X, 1, 2)
% This computes the difference along the second dimension (rows).

Common errors when using diff include confusion over the dimensions of input arrays and forgetting that the output size of Y will always be less than X. The output length will be length(X) - 1 for vectors, which can sometimes lead to unexpected results if not accounted for.

In conclusion, mastering the diff function in MATLAB permits users to execute essential operations such as numerical differentiation and data analysis effectively, enhancing their capabilities in programming and data science.

Watch Complete Tutorial on MATLAB 0de45

In this video, we dive deep into solving ordinary differential equations (ODEs) in MATLAB online, focusing on three powerful tools: diff dsolve and ode45. Whether you’re new to MATLAB or looking to enhance your skills, this tutorial covers the essential theory behind ODEs, as well as practical demonstrations on how to apply these functions to real-world problems.

In this video, we cover:

• A detailed introduction to ordinary differential equations (ODEs) theory and their importance in mathematics and engineering.
• How to solve ODEs symbolically using MATLAB’s dsolve function, and understand the solutions it provides.
• The basics of the ode45 solver in MATLAB, a versatile function for solving complex numerical differential equations and initial value problems (IVPs).
• Step-by-step demonstrations of applying ode45 for solving first-order and second-order differential equations, including systems of ODEs.
• Tips for choosing the best MATLAB ODE solver based on your problem, including using ode45 for accuracy and speed.

By the end of this tutorial, you’ll be able to:

• Understand the core concepts behind ODEs and how to solve them using MATLAB solvers.
• Use dsolve to obtain exact symbolic solutions for differential equations.
• Master ode45 for efficient numerical integration and solving a wide range of ODE problems in MATLAB.

Learn MATLAB with Online Tutorials

Explore our MATLAB Online Tutorial, your ultimate guide to mastering MATLAB! Whether you’re a beginner or an advanced user, this guide covers everything from basic MATLAB concepts to advanced topics

Practical Use Cases for MATLAB Diff

The MATLAB diff function serves various practical applications across multiple fields, facilitating essential data analysis tasks. In engineering, for instance, professionals frequently rely on the diff function to analyze sensor data. By calculating the differences between successive measurements, engineers can swiftly identify trends, detect anomalies, and assess system performance over time. This capability is crucial for predictive maintenance, where early detection of anomalies can mitigate costly downtime.

In the realm of finance, MATLAB diff finds extensive application in analyzing stock market data. Financial analysts utilize this function to compute daily returns based on historical price data. By deriving the difference between current and previous prices, analysts can gauge volatility and forecast future price behavior. These insights enable small business owners invested in financial markets to make more informed investment decisions, maximizing their potential returns while managing risk.

Similarly, in the field of biology, researchers employ the diff function to analyze biological data collected over time. For example, when studying population dynamics, biologists can use MATLAB to calculate the change in population size from one time point to the next. This discrete change helps in modeling growth rates and understanding ecosystem dynamics. By interpreting these fluctuations, small business owners engaged in sustainable agriculture or ecotourism can make informed decisions about resource management and conservation efforts.

Additionally, the integration of the diff function in time series analysis allows for extracting essential insights from complex datasets. Small business owners can leverage these insights to enhance operational efficiency, optimize resource allocation, and innovate product offerings based on data-driven trends. Thus, the application of MATLAB diff across diverse fields showcases its capacity to improve decision-making processes and drive informed strategies within various business contexts.

Tutorial on Newton Raphson Method in MATLAB

Implementing the Newton-Raphson method in MATLAB is a straightforward process and allows for the automation of iterative calculations. MATLAB’s rich libraries and intuitive interface facilitate the coding of the algorithm, providing users with the tools to explore complex functions. By leveraging MATLAB’s capabilities, one can easily handle numerical computations and visualize the convergence of the method, thus deepening the understanding of its mechanics and applications.

Learn to Implement Newton Raphson Method in MATLAB

Tutorial on Euler Method in MATLAB

One of the key advantages of the Euler method is its simplicity and ease of implementation, particularly in programming environments such as MATLAB. Learn to Implement Euler Method in MATLAB

The method allows for a rapid computation of approximate values, making it a popular choice for introductory courses in numerical methods. the Euler method, named after the Swiss mathematician Leonhard Euler, is a fundamental numerical technique widely used in mathematical analysis for solving ordinary differential equations (ODEs).

Advanced Techniques

The diff function in MATLAB is a powerful tool that goes beyond basic differentiation, offering advanced techniques that can be useful for data scientists and programmers. This section delves into higher-order differentiation and numerical differentiation, which are particularly valuable when working with complex datasets.

Higher-order differentiation is the process of finding the derivative of a derivative. In MATLAB, you can achieve this by applying the diff function multiple times. For example, if you have a signal defined as a vector y = [3, 6, 9, 12, 15], and you want to perform second-order differentiation, you would write:

y_first = diff(y)
% First derivative
y_second = diff(y_first)
% Second derivative

This approach not only provides insight into the curvature of your data but also helps in identifying trends and making predictions. Each application of the diff function reduces the length of the input vector, which is critical to consider when handling results in subsequent analyses.

On the other hand, numerical differentiation is essential when dealing with discrete data points where analytic differentiation is not feasible. MATLAB offers the gradient function, which provides a numerical approximation of derivatives. For instance, if you have time series data, you can estimate the first derivative, which provides the rate of change of your dataset:

t = [0, 1, 2, 3, 4]
% Time vectory = [0, 1, 4, 9, 16]
% Data pointsdy_dt = gradient(y, t)
% Numerical differentiation

It is highly recommended to visualize the results of differentiation using MATLAB’s plotting functions. This will enhance the interpretability of complex datasets. By incorporating these advanced techniques, data scientists can effectively leverage the full capability of the matlab diff function, leading to better insights and decisions derived from data analysis.

Integrating MATLAB Diff with Other Functions

Utilizing the matlab diff function effectively requires an understanding of how it can be combined with other MATLAB functions to create a versatile data analysis workflow. This integration allows users to perform comprehensive analyses that cater to both simple tasks and complex data models. For instance, the diff function can be used in tandem with the mean and std functions to analyze trends in a dataset. By first applying diff to calculate differences between data points, one can then compute the mean and standard deviation of these differences, providing valuable insights into data variability.

Moreover, coupling matlab diff with visualization tools such as plot can enhance data representation. After calculating the differences in a dataset, a line graph or scatter plot can be generated to visualize trends and anomalies effectively. For example, after obtaining the first derivative of a dataset representing temperature over time using diff, this information can be plotted to visualize the rate of change, thereby providing an intuitive understanding of fluctuations within the data.

Furthermore, integrating diff with functions like filter can enable more advanced analyses. By diminishing noise in data, the filtering process can precede the application of diff, leading to cleaner results and more accurate insights. This approach allows users to observe the underlying trends without being misled by spurious fluctuations resulting from noise.

Additionally, using matlab diff in conjunction with the findpeaks function can uncover significant local maxima and minima in the data. Identifying these points often proves critical in fields like signal processing and financial analysis, where recognizing changes in behavior or trends is vital. By harnessing these integrations, users can unlock the true potential of MATLAB to tackle both straightforward and intricate data analyses.

MATLAB conv2 Function

Convolution is a mathematical operation that combines two functions to produce a third function, expressing how the shape of one function is modified by the other. Convolution is calculated using MATLAB conv2 function. This operation is particularly crucial in various fields such as image processing, signal analysis, and systems engineering. This function is specifically designed for two-dimensional convolution, making it preferable for tasks that involve images or other matrix-based data

fft2 in MATLAB

The FFT2 function in MATLAB is crucial for performing Fourier transforms on matrices, allowing practitioners to study and manipulate two-dimensional frequency components effectively. The Fast Fourier Transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) and its inverse efficiently. The DFT converts a sequence of equally spaced samples of a function into a sequence of coefficients of sinusoidal components, revealing the frequency spectrum of the sampled signal.

fzero MATLAB Function

The fzero in MATLAB is a powerful tool designed for finding the roots of nonlinear equations. This function plays a crucial role in various fields, including engineering, data science, and mathematical modeling. By utilizing fzero MATLAB, users can efficiently identify points where a given function equals zero, which is essential for solving problems that involve polynomial equations, differential equations, and optimization tasks.

MATLAB interp1 Function

The interp1 function in MATLAB serves as a fundamental tool for conducting one-dimensional interpolation on a set of data points. Interpolation is a statistical method that estimates values between two known values, allowing for more precise data analysis and management. By employing the interp1 function, users can obtain interpolated values at specified points, thus enabling a deeper analysis of datasets.

Troubleshooting Common Issues with MATLAB Diff

When utilizing the MATLAB diff function, users may encounter a range of challenges that can impact their workflow and the effectiveness of their data analysis. A common issue is misunderstanding the output dimensions, especially when applying the diff function to multi-dimensional arrays. Users may expect the output to match the dimensions of the input, but due to how MATLAB computes differences, the result will always have one less element along the dimension being operated on. To remedy this, always verify the dimensions of the input data before application, and ensure you understand the implications of the output’s shape.

Another frequently encountered error is the incorrect data type being fed into the diff function. For example, string arrays or cell arrays will not produce the desired numeric differences. It is crucial to check the data type of the input before calling the diff function. Converting input data to the appropriate type using functions like cell2mat or str2double when necessary can prevent these issues. Additionally, users should take note of NaN values in their datasets; these can lead to unexpected results or even errors in some cases. Using isnan to check and handle NaN values provides a more robust analysis.

Moreover, users may overlook the option of specifying the dimension along which to compute the difference. By default, MATLAB operates along the first non-singleton dimension; however, this can lead to unintended results if the data structure does not align with the users’ expectations. Leveraging the dimension parameter in the diff function enhances control over the results. Lastly, familiarity with the function’s documentation and error messages can significantly reduce troubleshooting time, as these resources provide valuable insights into the usage and limitations of the diff function.

Recommended Tools and Resources for Further Learning

To effectively master the MATLAB diff function and expand your knowledge of data analysis in MATLAB, an array of resources is available that cater to varying levels of expertise. This subsection provides a curated list that can facilitate your learning journey.

Firstly, the official MATLAB documentation is an indispensable resource. It provides comprehensive details about the diff function, including syntax, parameters, and examples of practical use cases. By navigating to the MathWorks website, you will find an extensive set of tutorials that can establish a solid foundation in MATLAB programming. Additionally, the user community forums, regularly frequented by MATLAB users, can be invaluable for troubleshooting common issues and engaging in discussions regarding best practices.

Several online platforms also offer courses specifically tailored to MATLAB programming. Websites such as Coursera, edX, and Udacity host a variety of courses, from beginner to advanced levels, which include modules on using the diff function for data analysis. These interactive courses often include assignments and quizzes that reinforce learning and provide hands-on experience.

Books such as “MATLAB for Data Analysis” and “MATLAB: A Practical Introduction to Programming and Problem Solving” are highly recommended. These texts delve deeply into MATLAB functionalities, including detailed explanations and examples for the diff function, making them a relevant addition to your library.

Lastly, consider leveraging platforms like GitHub, where you can find repositories with open-source MATLAB projects. These projects often showcase practical applications of MATLAB functions, including diff, and can deepen your understanding through real-world examples. Furthermore, our own platform offers tutoring services aimed at enhancing your MATLAB knowledge, providing both online resources and one-on-one sessions to clarify concepts and improve your coding skills.

FAQs

The MATLAB diff function is frequently queried by both novices and experienced programmers alike. One common question is, “What does the MATLAB diff function do?” This function calculates the difference between adjacent elements in an array, providing valuable insights for various applications, such as numerical analysis and data processing. For instance, if you have a time series dataset, using MATLAB diff enables you to compute the rate of change over time, which is essential for trend analysis.

Another frequently asked question is, “Can MATLAB diff be applied to matrices?” Yes, it can. When applied to matrices, the diff function operates along a specific dimension, allowing you to obtain differences between rows or columns. This capability is particularly useful in multidimensional data analysis, where understanding changes across different variables is necessary for comprehensive evaluation.

For those concerned about performance, questions regarding the speed and efficiency of MATLAB diff are common. Given that MATLAB is optimized for matrix operations, utilizing the diff function can be very efficient. However, applying it on very large datasets may require consideration of memory usage and execution time. Users looking for more specific guidance often seek clarity on the best practices for employing MATLAB diff within their workflows. Ensuring that data is pre-processed appropriately and utilizing vectorized operations can significantly enhance performance.

Finally, as various industries employ MATLAB diff, questions related to its applications in fields such as finance, engineering, and data science also arise. Understanding how to leverage this function for insightful data analysis can provide significant advantages in these domains.

For additional assistance, we invite you to explore our comprehensive blog article featuring 60 detailed MATLAB examples. These examples are designed to help you enhance your understanding of MATLAB’s functionalities and application in various fields. Each example is thoughtfully selected to cover a range of topics, from basic syntax and operations to more advanced programming techniques, ensuring that learners at all levels can benefit from them. Whether you’re just beginning or looking to refine your skills, this resource will provide valuable insights and practical knowledge.