Introduction to Ode45 in MATLAB
Ode45 is a widely utilized numerical solver in MATLAB designed for the effective resolution of ordinary differential equations (ODEs). It is a part of MATLAB’s ODE suite and is specifically tailored to handle problems where the solution requires the calculation of derivatives at multiple points. The significance of Ode45 stems from its implementation of the Runge-Kutta method, which offers a robust approach to approximating solutions with high accuracy.
Ordinary differential equations represent relationships involving functions and their derivatives, frequently appearing in various fields such as physics, engineering, and economics. These equations describe dynamic systems, making them essential for modeling real-world phenomena. Solving ODEs analytically can be complex or even impossible for nonlinear cases; therefore, numerical methods provide an alternative route to obtaining feasible solutions.
Among the many numerical methods available, Ode45 holds a prominent position due to its versatility and efficiency. The algorithm adapts to the complexity of the problem by modifying step sizes during the computation, thus ensuring a balance between accuracy and computational cost. This feature is particularly advantageous for data scientists and engineers who often work with large datasets and require quick yet precise results.
The ease of use and integration of Ode45 into MATLAB environments further cements its status as a preferred choice among practitioners. With intuitive syntax and built-in features, users can quickly model and solve ODEs, leading to more efficient workflows in their data science tasks. Understanding the functionalities offered by Ode45 is a crucial step for anyone looking to leverage numerical solutions for ordinary differential equations in their programming and research endeavors.
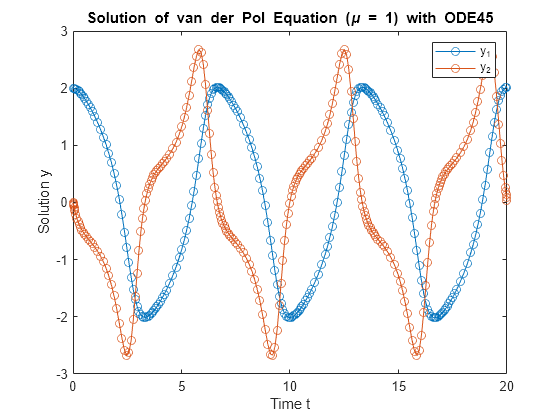
Step-by-Step Guide to Implementing Ode45 in MATLAB
Implementing ode45 in various programming environments can significantly enhance your capability to solve ordinary differential equations. Here, we will provide a detailed guide to help you navigate this process smoothly in both MATLAB and Python.
Starting with MATLAB, the ode45 function is widely used due to its efficiency and ease of use. To implement it, begin by defining your differential equation as a function. For instance, if you have the equation dy/dt = f(t, y), you would create a function file like so:
function dydt = myODE(t, y) dydt = -2 * y + t^2 end
Next, you will need to specify the interval for the solution and initial conditions. For example, if you want to solve the equation from t=0 to t=5 with an initial condition of y(0)=1, your code would look like this:
tspan = [0 5] y0 = 1 [t, y] = ode45(@myODE, tspan, y0) plot(t, y)
Parallelly, in Python, the implementation of ode45 can be achieved using the SciPy library, specifically the solve_ivp function, which serves a similar purpose. First, ensure you have the necessary library installed:
pip install scipy
You will then define the differential equation in a manner similar to MATLAB:
from scipy.integrate import solve_ivp import numpy as np import matplotlib.pyplot as plt def myODE(t, y): return -2 * y + t**2
Next, set your initial conditions and time span as follows:
t_span = (0, 5) y0 = [1] sol = solve_ivp(myODE, t_span, y0, t_eval=np.linspace(0, 5, 100)) plt.plot(sol.t, sol.y[0])
It is crucial to remember common pitfalls when dealing with ode45 or its Python equivalents. One frequent error is misdefining the differential function or neglecting to properly shape your initial conditions, which could lead to runtime errors or inadequate results. By following these step-by-step instructions, you can effectively implement ode45 and adapt it to fit various projects in both MATLAB and Python.
Meet Ahsan – Certified Data Scientist with 5+ Years of Programming Expertise
👨💻 I’m Ahsan — a programmer, data scientist, and educator with over 5 years of hands-on experience in solving real-world problems using: Python, MATLAB, R, SQL, Tableau and Excel
📚 With a Master’s in Engineering and a passion for teaching, I’ve helped countless students and researchers: Complete assignments and thesis coding parts, Understand complex programming concepts, Visualize and present data effectively
📺 I also run a growing YouTube channel — Algorithm Minds, where I share tutorials and walkthroughs to make programming easier and more accessible. I also offer freelance services on Fiverr and Upwork, helping clients with data analysis, coding tasks, and research projects.
Contact me at
📩 Email: ahsankhurramengr@gmail.com
📱 WhatsApp: +1 718-905-6406

Why Clients Trust Me – Real Stories, Real Results

“Ahsan completed the project sooner than expected and was even able to offer suggestions as to how to make the code that I asked for better, in order to more easily achieve my goals. He also offered me a complementary tutorial to walk me through what was done. He is knowledgeable about a range of languages, which I feel allowed him to translate what I needed well. The product I received was exactly what I wanted and more.” 🔗 Read this review on Fiverr
Katelynn B.
Solve Differential Equations in MATLAB using ode45, diff, and dsolve
In this guide, we dive deep into solving ordinary differential equations (ODEs) in MATLAB online, focusing on three powerful tools: diff dsolve and ode45. Whether you’re new to MATLAB or looking to enhance your skills, this tutorial covers the essential theory behind ODEs, as well as practical demonstrations on how to apply these functions to real-world problems. This tutorial is perfect for students, engineers, and anyone looking to get a deeper understanding of solving ODEs in MATLAB.
MATLAB ode45 function Tutorial
The ease of use and integration of Ode45 into MATLAB environments further cements its status as a preferred choice among practitioners. With intuitive syntax and built-in features, users can quickly model and solve ODEs, leading to more efficient workflows in their data science tasks. Understanding the functionalities offered by Ode45 is a crucial step for anyone looking to leverage numerical solutions for ordinary differential equations in their programming and research endeavors.
MATLAB diff function Tutorial
Moreover, MATLAB offers powerful tools for differentiation through MATLAB diff function, enabling users to compute derivatives analytically and numerically. This allows professionals and students alike to practically apply the concepts of differentiation in their projects, thereby bridging the gap between theory and real-world application.
In this guide, we will cover:
- A detailed introduction to ordinary differential equations (ODEs) theory and their importance in mathematics and engineering.
- How to solve ODEs symbolically using MATLAB’s dsolve function, and understand the solutions it provides.
- The basics of the ode45 solver in MATLAB, a versatile function for solving complex numerical differential equations and initial value problems (IVPs).
- Step-by-step demonstrations of applying ode45 for solving first-order and second-order differential equations, including systems of ODEs.
- Tips for choosing the best MATLAB ODE solver based on your problem, including using ode45 for accuracy and speed.

When to Use Ode45
Ode45 is a well-known MATLAB function designed for solving ordinary differential equations (ODEs) using the Runge-Kutta method. It excels in scenarios where the function’s behavior is complex and may change rapidly, making it a strategic choice for data scientists and engineers alike. This method is particularly effective when one is faced with initial value problems for both stiff and non-stiff ODEs.
One of the primary characteristics that make Ode45 an optimal method is its adaptive step size feature. This enables the algorithm to adjust the resolution of the solution automatically, refining the steps during calculation to ensure accuracy in regions where the solution changes swiftly. Consequently, when working on problems such as population dynamics or chemical reaction rates—where rapid changes can occur—Ode45 provides a reliable solution path. Its ability to solve problems efficiently without significantly increasing computational time sets it apart from other numerical methods, such as Euler’s method, which can be less accurate and require a cumbersome step size selection process.
Moreover, Ode45 applies well to a diverse range of applications in MATLAB, making it a valuable tool in both academic and industry settings. For instance, in individual projects, you might use Ode45 to simulate a mathematical model representing physical phenomena, like the motion of a pendulum under varying forces. In business solutions, it might be implemented in financial modeling, where understanding the continuous change in investment returns is crucial. By employing Ode45 in these contexts, one can achieve precise solutions that enhance decision-making processes and improve overall project outcomes.
How Ode45 Works: The Underlying Algorithm
The Ode45 algorithm is a widely used tool in numerical analysis, particularly tailored for solving ordinary differential equations (ODEs). At the core of this method lies the Runge-Kutta technique of order 5(4), which strikes an effective balance between accuracy and computational efficiency. By employing a combination of multiple evaluations of the function at several points within each integration step, Ode45 adeptly approximates the solution to an ODE.
One of the primary components in the working of Ode45 is timeframe discretization. The continuous time domain of the differential equation is divided into discrete intervals, allowing the algorithm to compute the solution incrementally. The size of these intervals—also referred to as time steps—is not predetermined; instead, it is adaptively adjusted depending on the behavior of the solution within the specified interval. This adaptability is a significant feature of Ode45, as it means that smaller time steps can be employed in regions where the solution fluctuates rapidly, while larger steps can be used where the solution is relatively stable.
The adaptive step sizing mechanism is closely linked to the algorithm’s error tolerance criteria. Ode45 assesses the local truncation error by calculating the solution at both the fourth and fifth order. If the computed error exceeds the specified tolerance, the algorithm reduces the step size and reruns the calculation for that segment. By continuously monitoring and managing the error associated with the solution, Ode45 ensures a high level of accuracy without unnecessarily increasing computational load.
This dual approach of adaptive steps alongside thorough error assessment allows MATLAB Ode45 to efficiently converge on reliable solutions, making it a preferred choice in various applications within data science and programming. The combination of these techniques greatly enhances the algorithm’s capabilities for a wide range of ordinary differential equations.
Learn MATLAB with Free Online Tutorials
Explore our MATLAB Online Tutorial, your ultimate guide to mastering MATLAB! his guide caters to both beginners and advanced users, covering everything from fundamental MATLAB concepts to more advanced topics.

Real-World Applications of Ode45 in MATLAB
Ode45, an advanced numerical integration tool based on the Runge-Kutta method, finds diverse applications across various fields, demonstrating its versatility and effectiveness in solving complex ordinary differential equations (ODEs). This section delves into several real-world applications of ode45 in engineering, physics, biology, and finance, showcasing its practical utility through case studies.
In engineering, ode45 is invaluable for simulating dynamic systems. For instance, mechanical engineers often use it to model the motion of rigid bodies. A notable case involved the analysis of a suspension bridge. By employing ode45, engineers were able to predict the system’s response to various loads and environmental conditions, allowing for optimization of the design and ensuring safety compliance without extensive trial-and-error testing.
Physics also benefits greatly from ode45, particularly in modeling the dynamics of systems. A case study that stands out is the simulation of projectile motion. Researchers used ode45 to analyze the trajectories of various projectiles under the influence of gravity and air resistance. This enabled them to derive insights into optimal launch angles and velocities, enhancing performance in both recreational and competitive shooting environments.
In the field of biology, ode45 is frequently utilized for modeling population dynamics. One example involved ecologists studying the interactions between predator and prey species. By employing this numerical solver, they developed differential equations that described population changes over time, leading to a better understanding of ecosystem stability and species conservation strategies.
Finance also leverages ode45 for risk assessment and option pricing. Analysts have successfully modeled financial derivatives using ordinary differential equations, allowing for more accurate predictions and pricing strategies. By applying ode45 to these equations, firms can manage risks associated with volatile markets effectively.
Through these diverse applications, ode45 proves to be an indispensable tool for tackling complex problems across multiple disciplines, showcasing its capability to drive impactful outcomes.
Common Challenges and How to Overcome Them
When utilizing the ode45 function, users often encounter several challenges that can hinder performance and lead to suboptimal results. One common issue is convergence problems, where the algorithm fails to find a solution within the specified tolerances. This situation often arises due to inadequate time-stepping or improper parameter settings. In such cases, it is vital to review the initial conditions and the function being solved, ensuring that they are correctly formulated and well-defined. Ensuring the correct scaling of state variables can also greatly enhance convergence.
Another frequent challenge is related to stiffness in the differential equations being solved. Ode45 is primarily designed for non-stiff problems; therefore, if stiffness is suspected, transitioning to a more appropriate solver such as ode15s may be necessary. Moreover, implementing adaptive step-size control can significantly improve the computational efficiency of ode45, allowing it to better handle problems that exhibit rapid changes or discontinuities.
Parameter settings, including the absolute and relative tolerances, play a crucial role in the performance of the ode45 solver. Users should experiment with these settings, adjusting them based on the specific dynamics of the problem. For instance, reducing the tolerances might lead to more accurate results, but at the expense of increased computation time. It is advisable to find a balance that suits the requirements of the given problem.
To further enhance the performance of the ode45 function, consider employing event functions to manage particular conditions that may arise during simulation, allowing for precise control over when to halt integration. Lastly, thoroughly reviewing the corresponding documentation and leveraging community resources can provide additional insights and solutions to any challenges encountered when using ode45.
MATLAB Ode45 in Comparison with Other Solvers
When working with ordinary differential equations (ODEs), selecting the appropriate numerical method is paramount to achieving optimal results. Ode45, a widely utilized solver in the MATLAB environment, stands out for its versatility and performance in various scenarios. This section examines Ode45 in relation to other notable solvers such as Ode23 and Ode15s, highlighting their respective strengths and weaknesses.
Ode45 is based on the Runge-Kutta method and is particularly effective for problems where precision is necessary. Its adjustable step size allows it to balance speed and accuracy well, making it suitable for a broad range of ODEs, especially those exhibiting smooth solutions. This adaptability gives it a significant advantage in many applications, from engineering to data science.
In contrast, Ode23 is more efficient for problems that are less demanding precision-wise. It employs a lower-order method, which can compute solutions more quickly, making it preferable for simpler ODE scenarios or when computational resources are limited. However, its simplicity may lead to poorer performance when applied to more complex equations requiring higher accuracy.
On the other end of the spectrum is Ode15s, which is designed for stiff ODEs that often arise in specific physical simulations or in mathematical modeling contexts where rapid changes in the system dynamics can create instability in solutions. Ode15s uses a variable order solver, which can be advantageous for maintaining stability, but it might not perform as well in non-stiff problems compared to Ode45.
In summary, while Ode45 is a robust solver suitable for many scenarios, understanding the nature of the differential equations at hand is crucial. For simpler needs, Ode23 may suffice, while Ode15s becomes essential in tackling stiff equations. This comparative analysis shows the importance of selecting the appropriate solver based on the specific characteristics of the ODEs being solved.
Advanced Functions in MATLAB Beside Ode45
Ode45 is a widely-used numerical solver designed for solving ordinary differential equations (ODEs) using the Dormand-Prince pair of methods. While it offers a robust and user-friendly interface, advanced techniques such as diff function in MATLAB can significantly enhance its performance and adaptability for complex applications. One such technique involves customizing the tolerance levels. This allows users to control the accuracy of the results, which is particularly beneficial for problems that exhibit rapid changes or stiffness. By adjusting the relative and absolute tolerance parameters, users can find a balance between computational cost and the precision of the solution.
Another advanced technique involves integrating Ode45 with other numerical methods to tackle more complex ODE systems. For instance, when dealing with systems that have varying stiffness, users can employ adaptive methods wherein Ode45 handles the non-stiff components while using a different method, such as ode15s or ode23s, for the stiff components. This hybrid approach not only optimizes the computational time but also enhances the stability and accuracy of the solution across the entire system.
Optimizing computational efficiency for large-scale problems is also paramount. One effective strategy is to leverage parallel computing resources. By splitting the ODE systems into smaller, independent segments, users can run Ode45 across different processors, significantly reducing overall execution time. Furthermore, implementing preconditioning techniques can minimize the numerical effort required for solving large systems. Techniques such as scaling the variables or using efficient initial guesses can greatly improve performance and convergence rates.
These advanced techniques facilitate a more comprehensive application of Ode45 in various data science and programming contexts. By customizing tolerance levels, integrating with other methods, and optimizing computation, practitioners can effectively tackle challenging problems that require enhanced numerical solutions.
MATLAB conv2 Function
Convolution is a mathematical operation that combines two functions to produce a third function, expressing how the shape of one function is modified by the other. Convolution is calculated using MATLAB conv2 function. This operation is particularly crucial in various fields such as image processing, signal analysis, and systems engineering. This function is specifically designed for two-dimensional convolution, making it preferable for tasks that involve images or other matrix-based data
fft2 in MATLAB
The FFT2 function in MATLAB is crucial for performing Fourier transforms on matrices, allowing practitioners to study and manipulate two-dimensional frequency components effectively. The Fast Fourier Transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) and its inverse efficiently. The DFT converts a sequence of equally spaced samples of a function into a sequence of coefficients of sinusoidal components, revealing the frequency spectrum of the sampled signal.
fzero MATLAB Function
The fzero in MATLAB is a powerful tool designed for finding the roots of nonlinear equations. This function plays a crucial role in various fields, including engineering, data science, and mathematical modeling. By utilizing fzero MATLAB, users can efficiently identify points where a given function equals zero, which is essential for solving problems that involve polynomial equations, differential equations, and optimization tasks.
MATLAB interp1 Function
The interp1 function in MATLAB serves as a fundamental tool for conducting one-dimensional interpolation on a set of data points. Interpolation is a statistical method that estimates values between two known values, allowing for more precise data analysis and management. By employing the interp1 function, users can obtain interpolated values at specified points, thus enabling a deeper analysis of datasets.
Conclusion and Next Steps
In this blog post, we have explored the fundamental aspects of the ode45 function, which is integral to solving ordinary differential equations (ODEs) in data science and programming. We began by discussing its utility in various computational scenarios, highlighting how ode45 employs variable time stepping and adaptive algorithms to deliver efficient solutions. Furthermore, we examined several practical applications, demonstrating the versatility of ode45 in fields ranging from engineering to finance.
Understanding ode45 is not just about mastering a function; it represents an essential skill for tackling complex problems requiring numerical solutions. By incorporating ode45 into your toolkit, you can significantly enhance your modeling capabilities, generating insights from data that were previously challenging to attain. As we move towards more intricate projects, mastering ode45 will serve as a foundation for deeper explorations into numerical methods and simulations.
As you embark on applying what you have learned, we encourage you to experiment with ode45 in varied scenarios. Consider working through additional examples, perhaps those related to your specific field of interest, to gain practical experience. Moreover, there is a wealth of resources available, including textbooks, online tutorials, and community forums dedicated to numerical computation methods. Exploring these materials will deepen your understanding and may provide solutions to any challenges you encounter.
If you require personalized assistance in leveraging ode45 for your data science and programming projects, feel free to reach out to our services. Our team is eager to assist you in transforming theoretical knowledge into practical application, ensuring that you achieve your project goals effectively. Happy coding, and we look forward to supporting you on your journey towards mastering ode45!
For additional assistance, we invite you to explore our comprehensive blog article featuring 60 detailed MATLAB examples. These examples are designed to help you enhance your understanding of MATLAB’s functionalities and application in various fields. Each example is thoughtfully selected to cover a range of topics, from basic syntax and operations to more advanced programming techniques, ensuring that learners at all levels can benefit from them. Whether you’re just beginning or looking to refine your skills, this resource will provide valuable insights and practical knowledge.